Hay que ser continuos, no puntuales.

Publicado el 6 de Julio de 2020 | Matemáticas

La continuidad es un concepto imprescindible para conseguir tus metas. Ser puntual es lo otra opción. En estadística todo funciona de manera puntual. Por eso soy impuntual, porque quiero ser continuo. Es continuo todo aquello que, si te acercas mucho, con una aproximación infinitesimal, resulta el valor del límite en ese lugar. La continuidad responde a todo aquello que no requiere de “levantar el lápiz”, es el concepto más visual. Por ejemplo, jugar a “unir los puntos” es recrearse en pasar de algo puntual, del mundo discreto, a algo continuo.

Las derivadas tratan el cálculo de variaciones de una función, el cálculo de máximos y mínimos y la convexidad. Hallar máximos y mínimos tiene una utilidad evidente en diversas áreas. Sacar el mínimo error, hallar un resultado máximo, o simplemente encontrar una singularidad es algo que define una curva, una estructura o cualquier expresión algebraica. Desde los astrónomos, para hallar planetas y los elementos que lo componen, hasta los físicos cuánticos, para hallar el bosón de Higgs, todos estudian lo que la derivación puede descubrir: singularidades. En lo diferente suele estar a lo más interesante. Una derivada es el cálculo de la variación instantánea de una función, también vista como la pendiente puntual de una curva, pero tanto el concepto de instante como de punto en algo continuo debe de ser visto como algo infinitesimal. No puedes medir un instante en nuestro mundo continuo, pero podemos aproximarnos todo lo que queramos, con esta formulación de la derivada de la función f en el punto x:

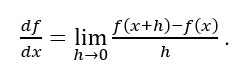
Esta notación es de Leibniz y, a partir del siglo XVII, el cálculo de derivadas nos llevó a ecuaciones con derivadas, lo que se llama cálculo diferencial, un área que revolucionó el mundo de las matemáticas.

Antes del siglo de Newton y Leibniz, las áreas y volúmenes se habían planteado a través de figuras geométricas, por las propiedades de los polígonos y poliedros. A partir del siglo XVII, el cálculo de áreas y volúmenes se haría a través de la integración. Para calcular el área que queda bajo una curva podríamos “pintar” ese recinto y calcular los trazos de línea empleados para “pintarlo” todo. He dicho pintar, sí, pero no es del todo cierto. Pintar sería, matemáticamente hablando, cubrir un recinto plano (de dos dimensiones), con trazos de cierta longitud, es decir, una línea finita (de una dimensión). A nivel práctico, parecería que una línea finita cubre el recinto, pero la realidad matemática es que un espacio de cierta dimensión no puede ser cubierto por un objeto de una dimensión inferior de forma finita, la línea en cuestión debería ser infinita. El error está en que la tinta genera un objeto con área, es decir, la línea que uno traza con un bolígrafo no es una línea en verdad, pues tiene área, tiene un trazo con un cierto grosor. La idea de integración es la de cubrir un espacio con un objeto de área conocida de una misma dimensión, de forma aproximada. Integrar es crear una suma infinitesimal que se ajusta al área o volumen buscado, y para eso tenemos los métodos, para encontrar una receta demostrada en ciertas situaciones. De aprender a cocinar con este recetario ya se encargan en la etapa Secundaria, aunque hay una verdad demoledora: hay más integrales que no sabemos resolver de las que sabemos resolver. Aprender métodos está muy bien, pero deberíamos ampliar al concepto de cálculo de integrales, con sus simbolitos y su planteamiento, que debemos por cierto a nuestro querido Leibniz.

Por Santiago García